Task Introduction
현업에서 머신 러닝 모델, 또는 딥러닝 모델을 사용할 때 실시간으로 수집한 사용자 데이터로 모델을 재 학습해야할 필요가 있습니다. 특히 사용자의 행동 패턴이 빠르게 변화하는 도메인이라면, 새로운 데이터를 수집해 실시간으로 모델을 업데이트 해 줘야 정확한 예측이 가능합니다.
이처럼 실시간으로 들어오는 데이터로 모델을 학습하는 것은 Online Learning이라고 합니다. 특히 서비스 초기에 학습 데이터가 아예 없는 상태 (cold-start)에서는 모델이 예측을 하면서 동시에 실시간으로 수집한 유저 데이터로 학습을 진행합니다. 즉, 하나의 모델로 예측과 학습을 동시에 하기 때문에 이를 single channel approach라고도 합니다.
통상적으로 말하는 머신 러닝, 또는 딥러닝 학습은 데이터를 Batch로 학습하는 경우를 말합니다. 즉, 학습 및 검증 데이터가 준비되어 있기 때문에 학습 데이터를 batch로 모델에 학습하면서 모델 층은 몇 개를 쌓아야하는지, 파라미터는 어떻게 맞춰야 하는 지 등을 검증 데이터로 검증을 하며 정할 수 있습니다. 그렇게 선택한 최종 모델을 배포하고 모델은 정해진 파리미터 값으로 예측만 수행합니다.
하지만 실제로 현업에서는 서비스 초기에 데이터가 없는 cold start 상황이 대부분 입니다. Online Learning은 이 상황에서 실시간으로 들어오는 학습 데이터로 어떻게 모델을 학습할 지에 대한 연구입니다.
Online Learning과 유사한 키워드로는
- Adaptive learning
- Online learning
- Active learning
- Transfer learning
- Incremental Learning
이 있습니다.
오늘은 Online Learning시 Hedge Backpropagation (HBP) 방법론을 제안한 Online Deep Learning: Learning Deep Neural Netwroks on the Fly (2017) 논문을 살펴보겠습니다.
Problems
논문은 Online Learning이 직면한 3가지 문제점을 제시했습니다.
- Batch 학습 데이터가 없기 때문에 모델(network)의 크기를 예측할 수 없다.
- 모델이 vanishing gradient 문제에 취약. Vanishing gradient 문제는 특히 모델의 레이어가 깊은 경우 여러개의 activation 함수를 거치면서 미분 값이 0에 수렴해져 파라미터 업데이트가 잘 이뤄지지 않아 학습 속도가 느려지는 문제를 말한다. Online learning시 모델은 학습을 하는 동시에 예측을 해야 하기 때문에 학습 속도 저하는 큰 문제이다.
- 모델이 Diminishing feature reuse 문제에 취약. Diminishing feature reuse는 vanishing gradient 문제와 유사한데 순전파 시 입력층과 가까운 layer의 feature가 출력값까지 전해지지 않는 문제를 말한다. 잎서 말했듯이 Online learning 모델은 학습 초기부터 예측을 하기 때문에 중요한 feature를 빠르게 찾고 그 영향력을 감소하지 않는 것이 중요하다.
Architecture
앞서 제시한 Online learning의 문제점을 해결하기 위해 논문은 Online Deep Learning (ODL) 이라는 학습 방식을 제안합니다.
ODL를 기존 L-hidden layer classifier 모델과 비교해 설명하겠습니다.
Deep Learning Classifier
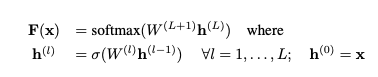
일반적인 (L-hidden layer) 딥러닝 분류 모델은 다음과 같이 정의할 수 있습니다.
- x: input ($x \in R^d$)
- $h^{(l)}$: l번째 hidden layer의 출력 값. 이전 layer의 출력값 ($h^{(l-1)}$)에 weight matrix ($W^{(l)}$)를 곱한 후 activation 함수 ($\sigma$) (sigmoid, relu, …)를 통과한 값.
- $F(x)$: 예측 값 ($\hat{y} \in R^C$, C는 label 개수). l번째 layer의 출력 값 ($h^{(l)}$)에 weight matrix ($W^{(L+1)}$)를 곱한 후 softmax를 취한 값.

모델의 예측 값과 실제 값의 차이는 loss fuction으로 정의합니다. Cross-entropy loss 함수를 $L(F(x), y)$로 정의할 때 l hidden layer의 parameter(W)를 업데이트하는 식은 위 그림과 같습니다. 즉, $W_t$에 대해 loss 함수의 미분값을 구해 learning rate를 곱한 만큼 파라미터를 이동합니다.
Online Deep Learning Classifier

ODL의 모델 아키텍처는 위 그림과 같습니다. 각 수식의 의미를 살펴보겠습니다.

위 그림은 순전파의 수식을 정리한 것입니다. $h^{l}$까지는 일반적인 딥러닝 모델과 동일합니다. 하지만 $\theta^{(l)}$ 과 $\alpha^{(l)}$ 파라미터가 추가됐습니다.
- x: input ($x \in R^d$)
- $h^{(l)}$: l번째 hidden layer의 출력 값. 이전 layer의 출력값 ($h^{(l-1)}$)에 weight matrix ($W^{(l)}$)를 곱한 후 activation 함수 ($\sigma$) (sigmoid, relu, …)를 통과한 값.
- $f^{(l)}$: 모든 layer의 $h^{(l)}$에 $\theta^{(l)}$ 파라미터를 곱한 후 softmax를 취한 값. 마지막 hidden layer의 출력값인 $h^{(L)}$ 에 output layer의 weight인 $W^{(L+1)}$를 곱해 softmax를 계산해 출력 값을 구한 것과 달리, 모든 hidden layer에 $\theta^{(l)}$ 파라미터를 곱해 softmax를 취해 $f^{(l)}$ 값을 구함. 아직 최종 출력 값은 아님.
- $F(x)$: 모든 hidden layer의 예측 값 $f^{(l)}$에 $\alpha^{(l)}$만큼 weight를 줘 더해 최종 예측 값을 생성. ($\hat{y} \in R^C$, C는 label 개수).
ODL 모델은 입력층까지 합해 (L+1)개의 layer마다 출력 값을 계산합니다. 따라서 loss 함수는 모든 layer의 출력값과 실제 정답의 차의 합으로 구할 수 있습니다.
![]()
결론적으로 ODL 모델은 3개의 파라미터를 업데이트해야 합니다. 파라미터 별로 업데이트 방식을 알아봅시다.
알파
Hedge Algorithm을 사용해 알파값을 업데이트 합니다.

학습 초기에 알파값은 uniform distribution 확률값을 값습니다.
$\beta \in (0,1)$는 discount rate parameter로 알파의 값을 베타의 loss 제곱 만큼 작게 만드는 역할을 합니다. 간단히 말해, 특정 laye의 loss가 크다면 그 layer의 영향력은 줄어들도록 학습합니다.
모든 layer의 알파값을 구한 후 정규화를 해 알파 값의 합이 1이 되도록 만들어 줍니다.
세타
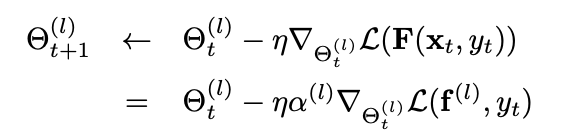
layer l의 loss 함수의 미분값을 알파 값과 곱해 update 크기를 구합니다.
W
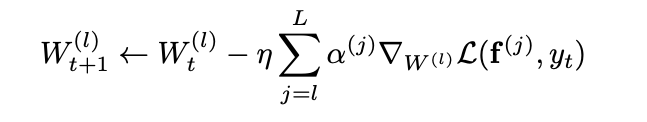
W를 업데이트 할 때는 해당 layer의 loss 함수만 미분을 하는 것이 아니라 해당 layer부터 마지막 layer까지의 loss 함수의 미분값을 모두 더해야 한다.
Results

표에서는 다양한 데이터 셋에 대해 학습 데이터를 점차 들려가면서 성능을 비교했습니다. 학습 초기에는 shallow model (L이 작은)이 더 좋은 성능을 보내주다가 데이터가 점차 쌓일 수록 deep model (L이 큰)이 더 좋은 성능을 보여주는 것을 알 수 있습니다. 이 처럼 학습 단계에 따라 최적의 모델 구조는 다른 것을 알 수 있습니다.
